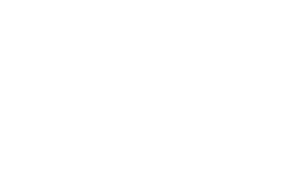Крадците се искачиле на првиот кат преку механичка платформа, пресекле прозорец, провалиле во две стаклени витрини и избегале пред да бидат забележани. Седум лица се веќе уапсени, но прашањето останува: како можеле да поминат незабележано во еден од најчуваните музеи во светот?
Директорката на музејот, Лоренс де Кар, призна пред францускиот Сенат дека системот за надзор бил сериозно ослабен: единствената камера што ја покривала терасата каде што се искачиле крадците била свртена во погрешен правец, а една третина од просториите во крилото Денон немале никакви безбедносни камери.
Иако алармите се активирале, како што наведе француското Министерство за култура, ова е трето големо ограбување на музеј во Франција за два месеца, што доведе до итни планови за нови мерки на заштита низ целата земја.

Интересно, еден геометриски проблем стар 50 години, познат како „проблемот на музејот“ или „проблемот на уметничката галерија“, се занимава токму со ова прашање – како со најмал можен број камери да се покрие целиот простор на музејот.
Решението, што го формулирал унгарскиот математичар Вацлав Чватал во 1973 година, гласи: ако просторот има n агли (врвови), тогаш доволно е n/3 камери за целосна покриеност, под услов секоја има 360° видливост.
На пример, галерија со 15 агли може целосно да се следи со само пет камери.
Неколку години подоцна, професорот Стив Фиск од колеџот Боудоин (САД) понудил елегантен доказ: со делење на просторот на триаголници и „бојадисување“ на аглите во три бои, доволно е да се постават камери само на аглите со една боја и просторот е целосно покриен.
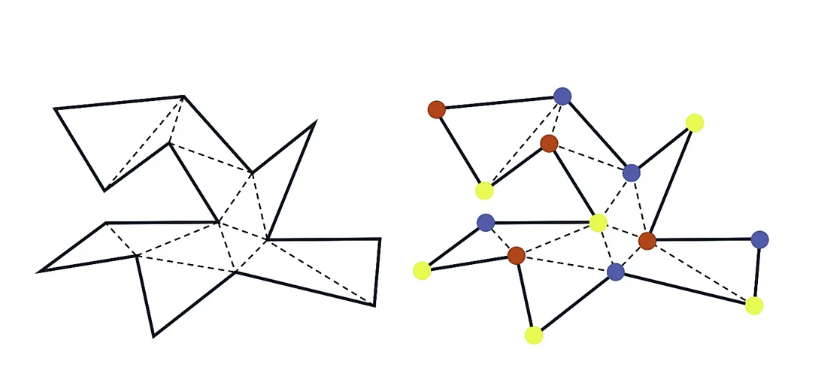
Во практична примена, вакви методи може да помогнат музеите да ги оптимизираат местата за поставување камери, намалувајќи трошоци и „мртви зони“.
Лоренс де Кар признала дека надворешните камери на Лувр не ги покривале сите ѕидови, поради што крадците можеле да се приближат незабележано. Математичката варијанта позната како „проблем на тврдина“ нуди решение и за надворешен надзор, пресметувајќи ги идеалните точки за целосна периметриска контрола.
По кражбата, музеите ширум светот почнаа повторно да ги преиспитуваат своите системи за надзор. Според експертите, принципите на „проблемот на музејот“ не се корисни само во безбедноста – тие се применуваат во роботика, урбано планирање, контрола на дронови, па дури и во осветлување на сцени и сали.
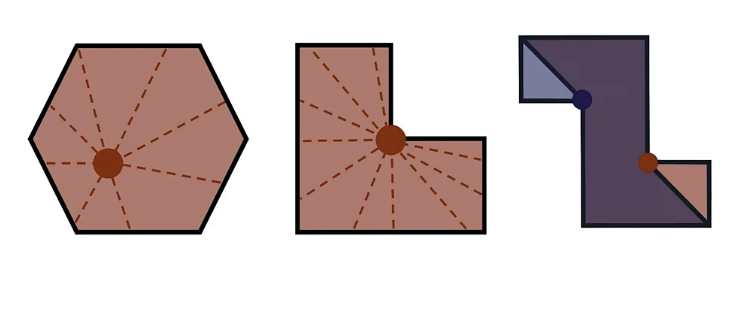
Иако Лувр не одговорил на прашањето дали ги разгледува овие математички решенија, јасно е дека едноставна формула од пред половина век можела барем делумно да го спречи најдрскиот уметнички грабеж во модерната историја на Франција.
Извор: BBC